Latitude and Longitude in the Real World

Radii of Earth in Geodesy

There are many places the radius of a sphere is used. For example it is used in the volume of the sphere. It also used to convert changes in direction from angular units to distances on the surface. An it has a physical meaning that is plain. The value is constant. It does not change with latitude.

For an ellipsoid these radii are different. And they are a function of latitude.

There are three common radii associated with the ellipsoid. The first is the physical radius, Re. The second, Rn, has a physical interpretation and is used to change longitude difference from angles to lengths. The third, often denoted Rm, is used to convert latitude differences to lengths. It has no easy physical interpretation.

Name	Symbol	Use
Physical	Re	Satellites,Gravity
Prime Vertical	Rn	Longitude
Meridian	Rm	Latitude

The meridian radius, properly called the radius of curvature in the meridian, is a complicated function of the derivatives of the ellipse. It is the radius of a circle that is just tangent to the ellipse at the desired latitude and has the same radius of curvature there.

The three radii are plotted as a function of latitude:

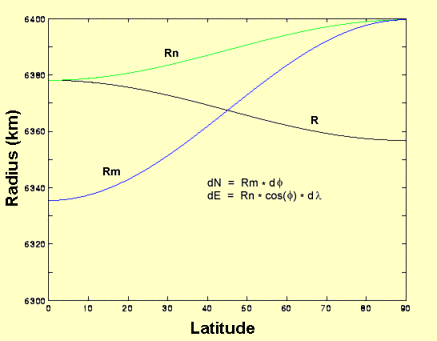
The formulae for conversion of the difference in latitude and longitude to lengths are given in the figure. In both cases these are the formulae for a sphere with all the radii equal to the physical radius.

For the longitude the formula applies to all differences of longitude. For latitude it only applies to small differences. For larger differences of latitude the small differences must be added up as Rm is a function of latitude. (The formula is integrated.)

These formulae apply to changes in north and east directions. For the general direction a more complex formula applies. Basically there is a radius of curvature at all azimuths and latitudes. In fact, if you deal in the inverse of the radii, the value is just the standard projection along the azimuth direction:

K(az) = Kn *cos(az) + Ke*sin(az)

where the K's are 1/R's, and az is the azimuth.

 

	Previous	Top	Next